Vibrated Fluids
The fluid research program at E-USOC is currently funded by the Ministerio de Economia y Competitividad (grant No. ESP2015-70458-P) with the purpose of investigating fluid phenomena induced by vibrations, which can play an important role in microgravity environments such as the International Space Station (ISS).
Understanding the effects of vibrations on confined fluid systems, whether gravity plays a big role or not, is critical to numerous scientific and engineering application in physics, chemistry, and biology. The response of the system naturally depends on physical properties of the fluid(s) involved, on the properties of the domain (i.e., boundary conditions) and on the characteristics of the applied excitation (frequency, amplitude and orientation). Periodic forcing, for example, can induce free surface instabilities like Faraday Waves, cross-waves, and frozen waves, while suppressing other phenomena like the Rayleigh-Taylor instability.
Pattern selection refers to the competition that may occur when the excited modes of the system occupy a lengthscale that is small compared to the extent of the domain, meaning that multiple states, with different spatial wavevectors and orientation, onset at (nearly) the same time. The fluid configuration that has attracted the most research in this field is the vertically forced Faraday system, where an open container of fluid of uniform depth with a stable flat interface is vibrated in a purely vertical fashion (i.e., perpendicular to the flat surface). These conditions, which imply that the initial state and the forcing are homogeneous and isotropic (in the infinitely extended limit), lead to theoretical simplifications and fluid behavior specific to that symmetry. More general forcing configurations, or more realistic treatment of the boundaries or meniscus waves, require these assumptions to be relaxed or dropped altogether. This is especially true in microgravity environments where the familiar preference for flat horizontal surfaces is absent.
Rapid vibrations can not only generate dynamics, like surface waves, on the same timescale, but will generally induce a slower (mean) reorientation of the fluid mass in response to the inhomogeneous oscillatory velocity field and the associated pressure gradient. This phenomena, which is especially pronounced in microgravity, is known as the vibroequilibria effect. In the limit of high amplitude, this effect will cause a free liquid interface to orient (nearly) perpendicular to the axis of vibration; such a restored preference for flat surfaces can be viewed as a type of artificial gravity (Beysens, Europhysics News 2004).
Experiments
Ground Experiments in the Fluids Lab: Surface Waves
Most experiments in the lab are performed using open containers of DC200 silicone oil or water. The container can be vibrated horizontally, vertically, or with any combination of the two, and at frequencies up to 100 Hz or more. Measurements of the surface wave patterns are obtained using a free surface synthetic Schlieren technique (Moisy et al. Exp. Fluids 46, 1021-1036, 2009).
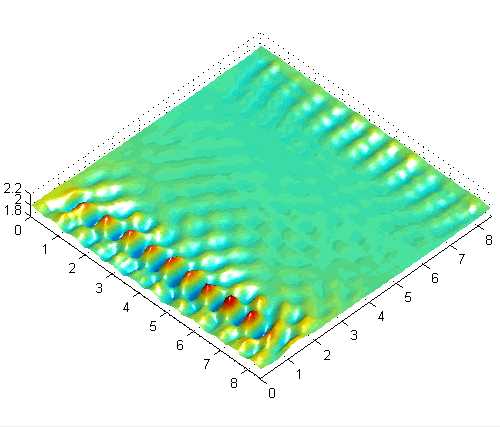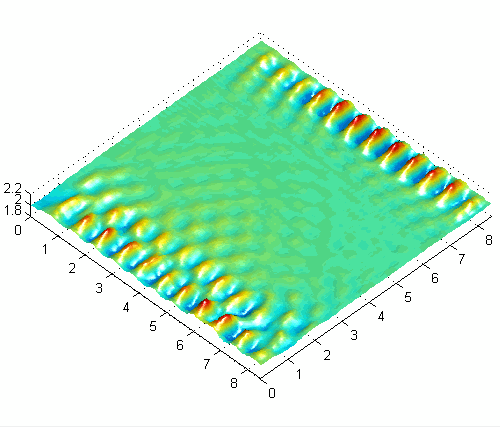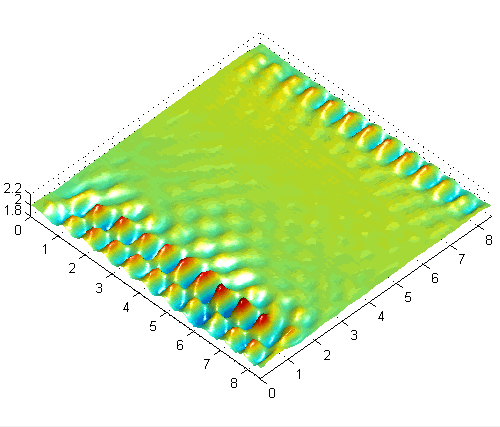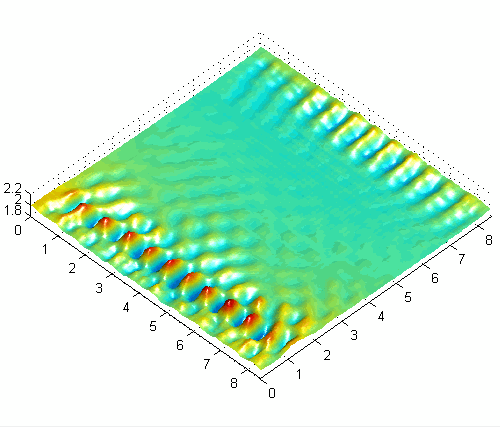
Asymmetric surface wave pattern with combined horizontal and vertical forcing at 50Hz
One basic experimental observation is the preference for obliquely oriented (rotated) cross-wave patterns with horizontally forcing [1]. The angle of these patterns depends somewhat on boundary conditions and other experimental parameters, but seems to be a very general and robust characteristic of subharmonic waves in large-aspect-ratio systems driven by moderate to high frequencies like those used here (30-100 Hz). Another interesting result with horizontally forced systems is the appearance of modulated (quasiperiodic) solutions [3] related to the interaction of the waves emanating from each endwall, which have a π/2 phase shift. The slowly modulated solutions alternate between one-sided and two-sided patterns and are very sensitive to the strength of the interaction (length of container, damping, detuning). With combined horizontal and vertical forcing, a variety of interesting new patterns and modulated solutions can be obtained and controlled with the forcing parameters.
An essential feature of any applicable theory in this regime is the distributed parametric forcing mechanism concentrated near each endwall. Previous cross-wave theory considered this mechanism to be sufficiently localized to be treated simply as a boundary condition on the slow spatial scale characteristic of streamwise variation. Without this assumption we obtain a nonlinear Schrodinger equation with spatially distributed forcing that is in reasonably good agreement with experimentally measured thresholds [3]. Other interesting features arising from the presence of distributed forcing include families of “cross-wave” modes (modulated or not) with the same crosswise mode number but separated by the number of oscillations experienced within the (supercritical) forced region and, when interaction is strong, additional branches of modulated solutions with distinct frequencies [2]. Much of the phenomenology can be understood in the context of simplified models that include essential features (like distributed forcing) and in terms of symmetry-breaking.
In addition, a horizontally vibrated container of fluid with sufficiently localized wave fields at each endwall (wavemaker) can be considered as an example of weakly coupled parametrically forced oscillators [4]. In the relevant case of two antisymmetrically forced oscillators, the primary instability is a Hopf bifurcation producing modulated solutions, like those observed in experiments [3]. Furthermore, the destruction of these modulated states via a saddle-node heteroclinic bifurcation in the model is consistent with numerical simulations of the Navier-Stokes equations.
To understand how the various surface wave instabilities investigated in the laboratory are altered in microgravity, extensive numerical simulations are done. These have revealed that the surface wave dynamics may affect the average surface shape (vibroequilibria) despite the apparent difference in timescales. Coupling is particularly strong when slowly modulated subharmonic surface waves are present, as these tend to drive an odd sloshing mode that can, in some cases, reach sufficient amplitude to completely destroy the underlying vibroequilibria state [5].
Control of Fluids in Microgravity with Vibrations (CFVib)
Microgravity experiments have recently been conducted as part of the 2016 Fly you Thesis! programme sponsored by the ESA Education Office [6]. These experiments were designed to test numerical and theoretical results related to vibroequilibria. The experimental set-up was organized around 12 containers (6 cuboids and 6 cylinders) having different liquid-air and liquid-liquid mixtures. Half were subjected to vibrations using a piezoelectric bender beam assembly (excited samples) while the other half (reference samples) were left to respond to the ambient inertial forces (g-jitter).
The main scientific objectives of the CFVib experiment are:
- Determine the feasibility of managing fluids using small amplitude vibrations in microgravity.
- Investigate the vibroequilibria effect in microgravity using different representative fluid configurations and forcing frequencies, including both hydrodynamic and acoustic regimes.
The experiment flew successfully in the 65th ESA Parabolic Flight campaign. In addition to providing very valuable experience in the design, construction and execution of a microgravity experiment, and an unforgettable experience for the participants, a large amount of promising accelerometer and video data was collected.
Snapshot of the first parabolic flight.
Source: Novaspace
Initial results indicate good qualitative agreement between experiment observations and the predictions of vibroequilibria theory and simulations. The expected dependence on the applied voltage to the piezoelectric device is observed in the videos. We expect this microgravity data to be very useful in the continued development and testing of theoretical models, and hope to continue with extensions of this microgravity research — perhaps in upcoming parabolic flight campaigns or aboard the ISS.
Selected references
- [1] J. Porter, I. Tinao, A. Laverón-Simavilla, and C. A. Lopez. Pattern selection in a horizontally vibrated container. Fluid Dyn. Res. 44, 065501 (2012).
- [2] J. Porter, I. Tinao, A. Laverón-Simavilla, and J. Rodríguez. Onset patterns in a simple model of localized parametric forcing. Phys. Rev. E 88, 042913 (2013).
- [3] I. Tinao, J. Porter, A. Laverón-Simavilla, and J. Fernández. Cross-waves excited by distributed forcing in the gravity-capillary regime. Phys. Fluids 26, 024111 (2014).
- [4] P. Salgado Sánchez, J. Porter, I. Tinao and A. Laverón-Simavilla. Dynamics of weakly coupled parametrically forced oscillators. Phys. Rev. E 94, 022216 (2016).
- [5] J. Fernández, I. Tinao, J. Porter and A. Laverón-Simavilla. Instabilities of vibroequilibria in rectangular containers. Phys. Fluids 29, 024108 (2017).
- [6] http://www.esa.int/Education/Fly_Your_Thesis/Student_experiments_on_parabolic_flights_performed_successfully.



